When you tell someone that you’re a mathematician or a mathematics professor, they invariably think that “you’re good with numbers”. Hence, it is inexcusable to be unable to make complex mental computations, and you’re basically doomed if you add or multiply numbers wrong.
Like most biases, though, such a conception is almost always far from the truth. Also like most biases, its origin is in a rushed generalization. Professional mathematics, namely the work of researchers, is so far from the mathematics we all study in school[1] that most of us can’t even imagine. And school mathematics, especially in the pre-university curriculum, is almost exclusively based on numeric computations. Hence the impression that professional mathematicians do the same kind of mathematics, only much harder problems and topics. And what could “much harder” mean but working with much larger numbers, right?
My aim here is not to debunk this bias. It would be too tedious to detail what a professional mathematician does and studies, let alone detail the branches of study and with all my efforts, I’m not sure such a topic would be popular. However, if you would like to read such an article, please let me know in the comments or via email and I promise to reply and write a detailed follow-up article.
“Numbers and Intuition” from the title refers to something else. While it may be true that some professional mathematicians are not very good at working quickly with numbers, small or large (I’m certainly one of them), however the abstract education and experience we gather make us harder to impress, so to speak, almost immune to surprising and counterintuitive truths. It is also true that we don’t often ask questions that a philosopher or an engineer or someone with a more concrete interest would raise such as: What is really the infinite or continuity? How many people could drink to their fullest from a cubic basin with a one-meter side? What are my chances of winning the lottery? My point is that working so often with highly abstract objects or topics and almost not caring for practical applications, one develops a kind of familiarity with abstract thought objects which, when one comes to think of them, are really impressive.
Numbers are such an example and again, I’m focusing on my experience alone. If in a rare numeric computation, I find a number such as 10100, I go on without even blinking or asking whether it could be about 10100 seconds, meters, stars, kilograms, or any concrete object, and what could it mean “in reality”.
What I will argue is that we don’t even need such big numbers to ensure huge surprises. But if we do reach such orders of magnitude, our imagination is simply overwhelmed. You’ve certainly heard or read this popular comparison: one million seconds means a bit over 11 days. One billion seconds is… more than 31 years! The million is 106, while the billion is 109. You may now guess that 10100, whatever it measured, would be a number that’s impossible to fathom let alone to give any concrete meaning.
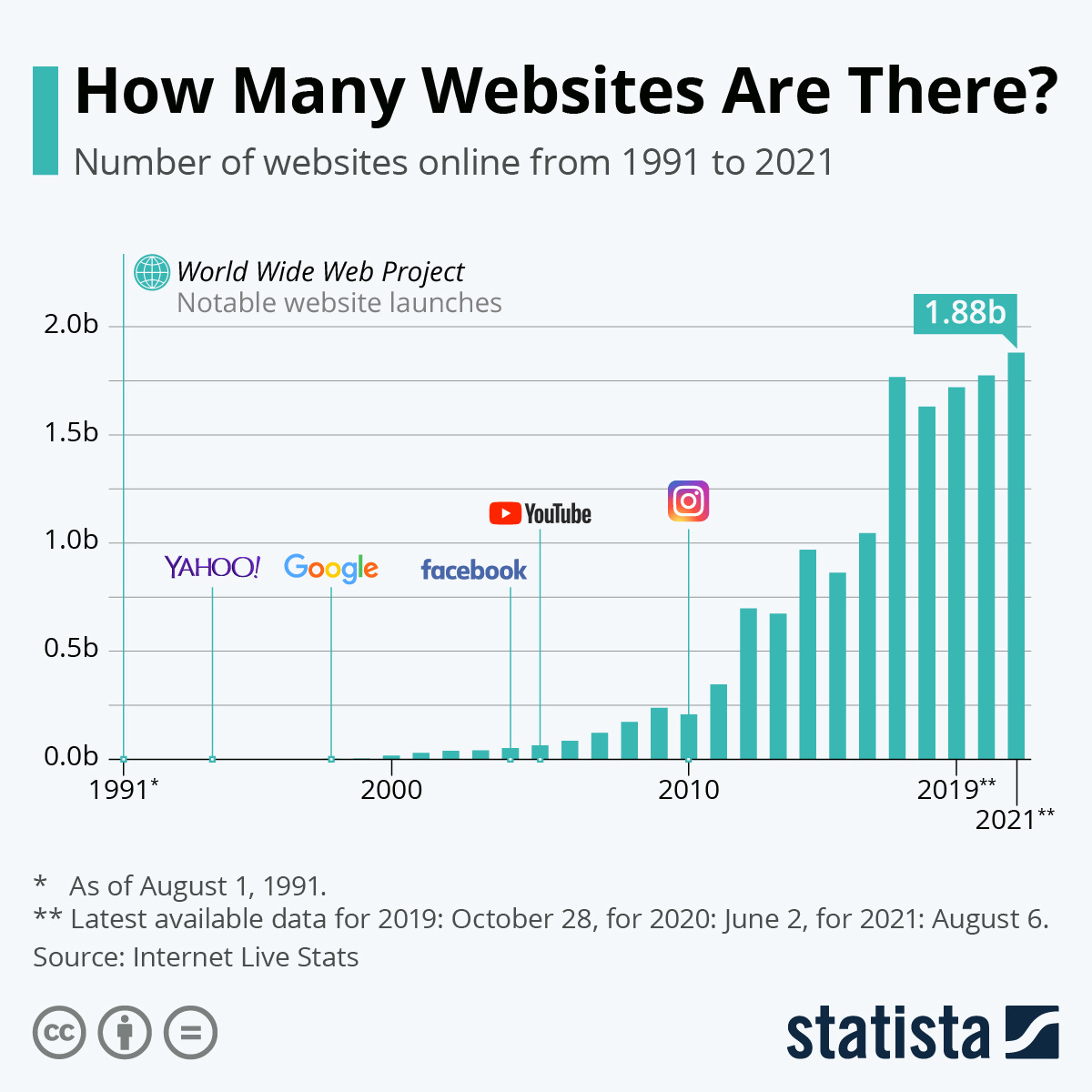
I should add that I haven’t chosen the number 10100 completely randomly; it is a number called a googol, a made-up word on which Google based its name. The founders chose it to mean that they could put order and help us search even among 10100 web pages. By the way, if you’re wondering how many web pages there are nowadays, the number is far from the famous googol. We can only count indexed web pages, meaning those which a search engine such as Google, Yahoo, Bing, or others could find, and in 2021, their total number was around 2 billion or 2×109, with an increase rate like in the picture.
Let’s round up the data therein and assume the number of websites doubles each year. Then the googol will be reached after more than 300 years!
Here’s another example, this time with a relatively smaller number, but equally counterintuitive. The number of ways one can rearrange n objects is computed using a mathematical object called a permutation, which is expressed using an operation called factorial. Its notation is n! and to obtain it, one has to multiply all positive integers from 1 to n. For example, 5! = 1×2×3×4×5 = 120. The factorial is a function with a surprisingly quick increase rate. So, let’s ask this question: how many possible arrangements are there for a deck of 52 cards? The answer is easy: 52!. Its value? Well… it has an order of magnitude of 1067. It’s a bit smaller than a googol, but how can one understand such a value? Does it compare to anything common? It is thought that the visible Universe contains 1024 stars. If each of these stars would give birth to a new identical Universe, with 1024 therein, we would only get to 1048, so we need a new “generation”: each of the newly created stars should give birth to a whole new Universe and only now have we reached 1072 objects. Another comparison: the total number of people who ever lived on the planet is estimated to be around 100 billion. The age of the Universe is about 13 billion years. The total number of minutes in a year is 525600. If we assume that there existed people who had playing cards in the very first second of the Universe and each of them shuffled that deck once every minute during the entire time of 13 billion years, they would have obtained only about 1027 possible shuffles. So there’s a big chance that if you shuffle a pack of cards today, the arrangement you obtain has never been obtained in the history of mankind and probably never will, for billions of years.
Finally, another popular example which works with a really small number refers to folding a piece of paper. Take any sheet of paper, say it’s an A4 format, and fold it in half. Repeat the procedure as many times as you can. Do you think you can do it 10 times in a row? What if the sheet is square with a one-meter side? Or even one-kilometer? Think of your own answer then read forward.
The problem here is not the area (namely the length and width of the sheet), but its thickness and more precisely, the ratio between the area and the thickness! A regular sheet of paper is around 0.1 mm thick, which is one-tenth of a millimeter. Every folding doubles its thickness and halves its area. 10 folds would mean doubling the thickness 10 times and halving the area 10 times in a row. In other words, this is a factor of 210 which is 1024: the area becomes 1024 times smaller, and the thickness becomes 1024 times larger. If we’re working with a 0.1 mm thickness, after 10 folds it becomes 102.4 mm, which is 10.24 cm. It’s not much, but the area becomes 1024 smaller, so if we assume that we have a sheet of paper of one square meter, 10 folds later it becomes 9.7 square centimeters in area and 10.24 centimeters in thickness; basically, we get a cube with a side of almost 10 centimeters. That’s why it’s practically impossible to complete the task without special equipment[2].
It is also worth mentioning that 100 folds would produce a factor of 2100, which has the order of magnitude of 1030. Here’s a comparison: the diameter of the observable Universe is approximately 1023 kilometers or 1029 millimeters. Hence, if the sheet of paper were 1 millimeter in thickness, after 100 folds it would become thicker than the entire Universe!
Now let us come back to the astonishment such examples create and draw a conclusion. We started by saying that most mathematicians’ work goes further and further away from numbers. At the same time, the abstract we manipulate so easily makes us not question too often the interpretation or concrete meaning of the computations or results we fiddle with. That’s why I decided to stop here at some simple computations and see that we don’t need sophisticated tools to obtain really impressive results. Amazement comes when we think practically, comparatively, or even intuitively about the orders of magnitude that such computations incur.
To sum up, one more thing could be added: the surprises that mathematics creates are closer than sophisticated and high-level applications. Numbers are still fascinating and if our ancestors may have thought of numbers of tens of digits in the class of the uncountable, the unending, the infinite, we now can “reach”, at least in our thoughts, such values and find that their concrete, “real” interpretation is amazing.
[1] Even number theory, also known as arithmetic, has evolved in a direction that is so abstract that numbers rarely appear anymore. Modern number theory uses algebra, analysis, even geometry and many more tools that are not really numeric. This doesn’t mean that the domain has changed its focus, but instead that the research problems have become so complex and so difficult that they do start with a numeric statement, but the proofs are almost always non-numeric.
[2] The Mythbusters team managed to do it working with special equipment and at an impressive scale, like they usually did.